An investigation of the dynamical transitions in harmonically driven random networks of firing-rate neurons

Abstract

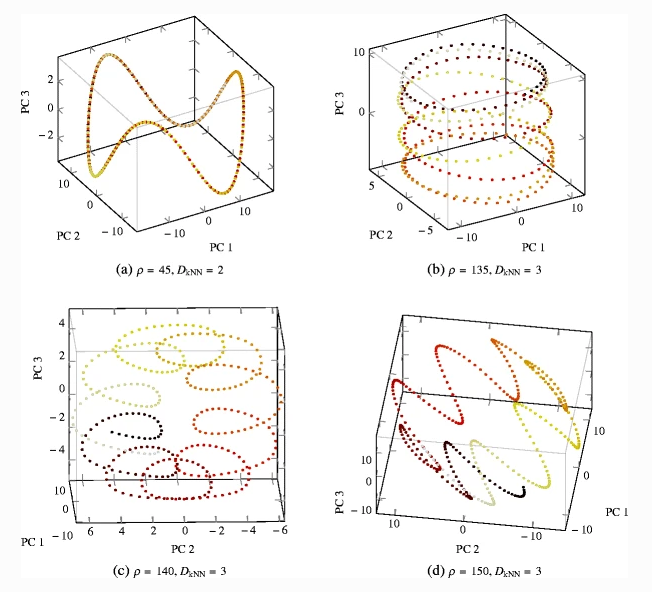
Continuous-time recurrent neural networks are widely used as models of neural dynamics and also have applications in machine learning. But their dynamics are not yet well understood, especially when they are driven by external stimuli. In this article, we study the response of stable and unstable networks to different harmonically oscillating stimuli by varying a parameter ρ, the ratio between the timescale of the network and the stimulus, and use the dimensionality of the network’s attractor as an estimate of the complexity of this response. Additionally, we propose a novel technique for exploring the stationary points and locally linear dynamics of these networks in order to understand the origin of input-dependent dynamical transitions. Attractors in both stable and unstable networks show a peak in dimensionality for intermediate values of ρ, with the latter consistently showing a higher dimensionality than the former, which exhibit a resonance-like phenomenon. We explain changes in the dimensionality of a network’s dynamics in terms of changes in the underlying structure of its vector field by analysing stationary points. Furthermore, we uncover the coexistence of underlying attractors with various geometric forms in unstable networks. As ρ is increased, our visualisation technique shows the network passing through a series of phase transitions with its trajectory taking on a sequence of qualitatively distinct figure-of-eight, cylinder, and spiral shapes. These findings bring us one step closer to a comprehensive theory of this important class of neural networks by revealing the subtle structure of their dynamics under different conditions.